[ 백준 BOJ / c++ ] 10971번 외판원 순회 2

🤔 문제

 

링크 : https://www.acmicpc.net/problem/10971

---

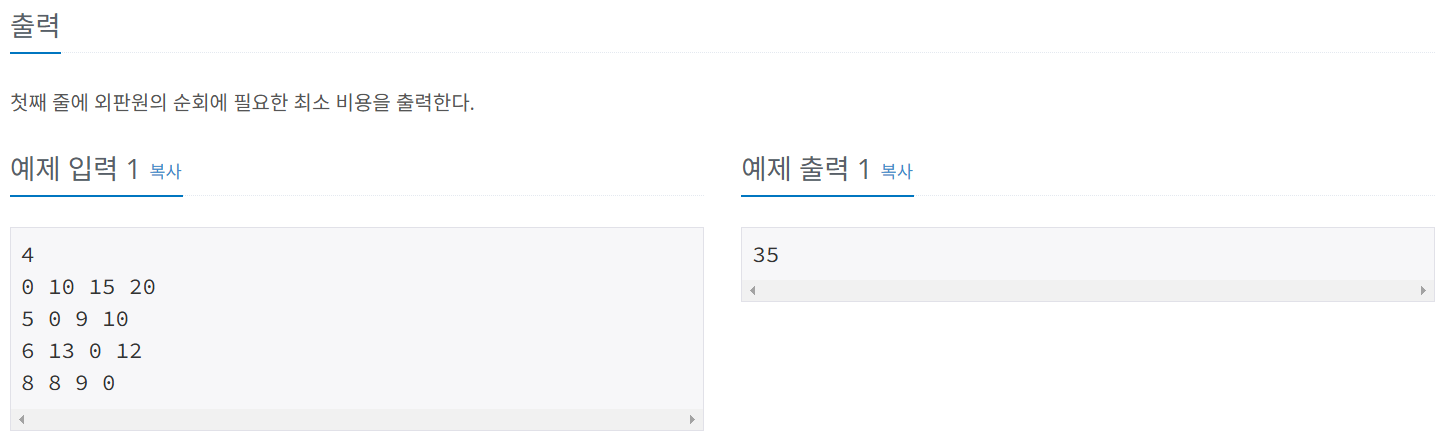
👀 접근 방식

먼저, 다음과 같이 설계하였다.

1. 모든 노드의 비중복 선택 경우의 수 를 계산
2. 마지막으로 선택된 노드에서 시작 노드로 돌아갈 가중치를 더해 최소값 찾기

1번 같은 경우, 백트래킹을 사용해 비중복 경우의 수를 구하였다.

백트래킹을 사용해 모든 경우의수를 구함

2번은 백트래킹이 끝나는 시점에 ( 시작노드 비용 ~ 마지막 노드 비용 ) 순으로 비용을 더한후 마지막 노드에서 시작노드로 돌아갈시 생기는 비용을 더해 순환 시 발생하는 총 비용 계산후 min함수를 통해 최솟값을 업데이트 하였다.

모든 비용 계산

 

추가로, 처음 제출시 오답이였는데, 이는 갈 수 없는 곳은 0으로 처리하기 때문이다. 즉, 다음과 같이 입력되면 0이 입력된 4행의 2번째 값을 알고리즘이 비용이 0인것으로 판단해 최소 비용이 달라지는 것이다. 

4
0 10 15 20
5 0 9 10
6 13 0 12
8 0 9 0

 

 

따라서 0이 입력되면 비용을 문제에서의 최대값인 1000001을 넣어주어 해결하였다.

 

---

💻 코드

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

bool visit[11];
vector<int> ans;
vector<int> inputs[11];
int n;
int _min = 10000000;

void dfs()
{
	// ans 벡터에 담긴 크기가 n개 일때
	if (ans.size() == n)
	{
		// 가중치 합 sum 선언
		int sum = 0;

		// ---- 가중치 합 계산 ----

		// ans 벡터의 가장 앞자리 노드 부터 시작해 가중치 계산
		int cur = ans[0];

		// 현재 노드에서 다음 노드의 가중치( value )를 sum에 계속 더한후, cur변수를 최신화 
		for (int i = 1; i < n; ++i)
		{
			int next = ans[i];
			int val = inputs[cur][next - 1];
			sum += val;
			cur = next;
		}

		// 마지막 노드에서 시작 노드의 가중치를 더함
		sum += inputs[cur][ans[0] - 1];

		// min 함수를 사용해 최소값 업데이트
		_min = min(_min, sum);

		//노드 출력 ( 디버깅 용 )
		/*for (int i = 0; i < n; ++i)
		{
			cout << ans[i] << " ";
		}
		cout << " -> sum : " << sum << '\n';*/
	}

	//1번 노드 부터 n번 노드에 대해 반복
	for (int i = 1; i <= n; ++i)
	{
		// i번째 노드에 방문하지 않았을 때
		if (!visit[i])
		{
			// i번째 노드를 방문처리
			visit[i] = true;

			// ans 벡터에 i번재 노드 번호 추가
			ans.push_back(i);
			// 다음 백트래킹 진행
			dfs();
			// ans 벡터 뒤에 값을 제외
			ans.pop_back();

			// i번째 노드를 비방문 처리
			visit[i] = false;
		}
	}

}

int main() {
	/*
		1. 모든 노드의 비중복 선택 경우의 수 를 계산
		2. 마지막으로 선택된 노드에서 시작 노드로 돌아갈 가중치를 더해 최대값 찾기
	*/

	// 노드 개수 n 입력 받기
	cin >> n;

	// 입력값 저장
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			int t; cin >> t;

			// 못가는 경우에 0이 입력된다 하였음으로, 가중치를 최대로 설정
			if (t == 0)
				t = 1000001;

			inputs[i].push_back(t);
		}
	}

	// 백트래킹을 사용해 비중복 선택 경우의 수를 구함
	dfs();

	//최소값 출력
	cout << _min;

	return 0;
}